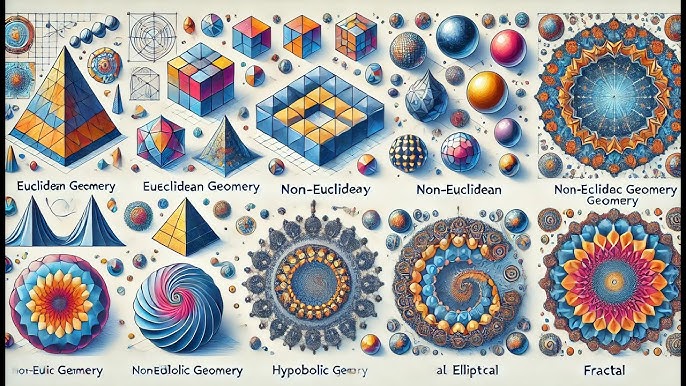
La geometría es una de las bases más antiguas y universales del conocimiento humano, pues estudia las propiedades, relaciones y medidas de las figuras en el espacio y en el plano. A lo largo de la historia, se han desarrollado diferentes tipos de geometría que responden a necesidades específicas: desde la construcción de templos y ciudades en la antigüedad, hasta la representación de formas complejas en la ciencia, el arte y la tecnología actual.
Cada tipo de geometría aporta un enfoque particular sobre cómo se conciben las formas, el espacio y las proporciones. Estas ramas se complementan entre sí y ofrecen múltiples herramientas para la creación, la organización visual y la resolución de problemas.
1. Geometría Euclidiana
Es la geometría clásica, formulada por Euclides en su obra Los Elementos (siglo III a.C.). Se centra en el estudio de puntos, rectas, planos y figuras planas o sólidas en un espacio bidimensional o tridimensional.
Sus principios básicos son:
- El punto como unidad sin dimensión.
- La línea recta como el camino más corto entre dos puntos.
- El plano como superficie infinita y sin grosor.
- Las figuras geométricas (círculo, triángulo, cuadrado, etc.) como construcciones ideales con proporciones exactas.
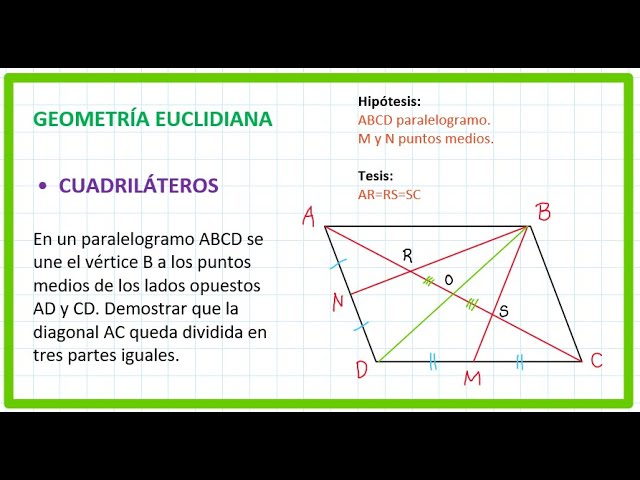
La geometría euclidiana es esencial porque permite trabajar con nociones de simetría, proporción, equilibrio y composición, aspectos fundamentales para organizar cualquier sistema visual.
2. Geometría Analítica
Introducida por René Descartes en el siglo XVII, combina la geometría con el álgebra mediante el uso de un sistema de coordenadas. A través de ella es posible representar cualquier figura geométrica con ecuaciones matemáticas.
- Permite ubicar un punto en el plano mediante coordenadas (x, y).
- Describe rectas, circunferencias, parábolas, elipses e hipérbolas a través de fórmulas.
- Ofrece un puente entre lo visual y lo numérico, lo que permite gran precisión en el diseño de estructuras y formas complejas.
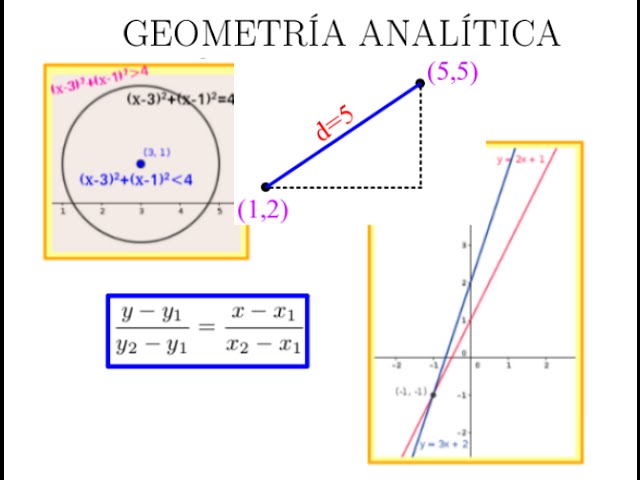
Es fundamental porque posibilita la representación exacta y controlada de figuras, más allá de lo perceptivo o intuitivo.
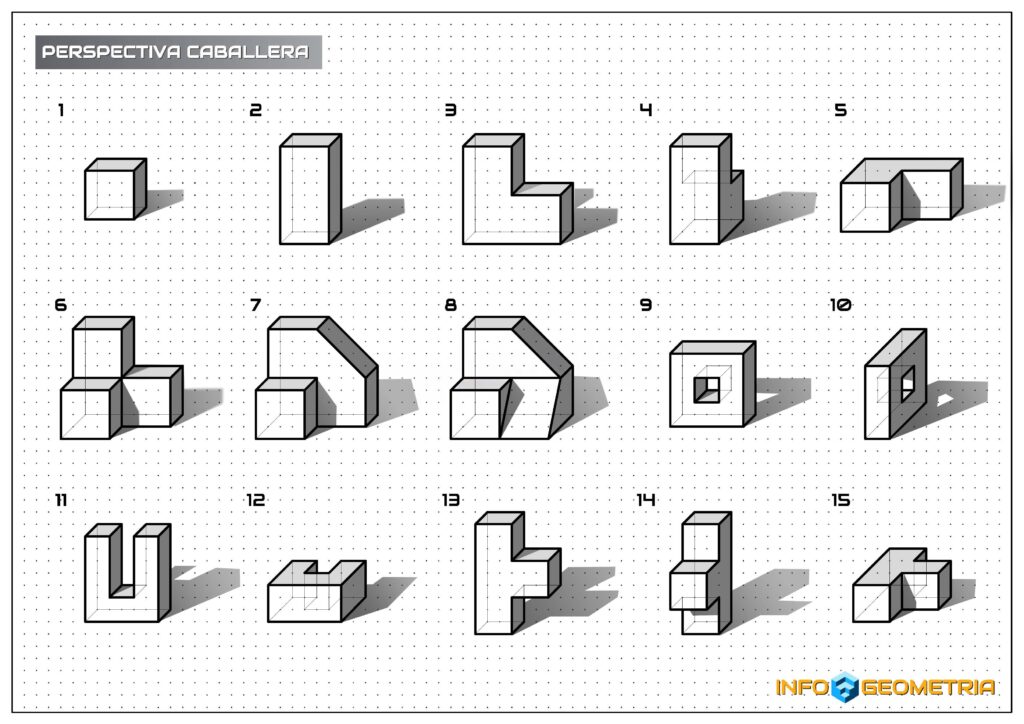
3. Geometría Descriptiva
Fue desarrollada en el siglo XVIII por Gaspard Monge. Su propósito es representar objetos tridimensionales en un plano bidimensional mediante proyecciones.
- Usa vistas ortogonales (frontal, superior, lateral).
- Emplea proyecciones axonométricas e isométricas.
- Permite comprender cómo un objeto en 3D puede representarse en papel o en pantalla con fidelidad.

Este tipo de geometría es clave para la transición entre lo tridimensional y lo bidimensional, lo cual resulta indispensable en procesos de representación técnica y visual.
4. Geometría Diferencial
Estudia las formas curvas y superficies complejas mediante el cálculo diferencial y el análisis matemático. Se centra en la curvatura, torsión y deformación de líneas y superficies.
- Permite comprender figuras que no se ajustan a las formas rectas o perfectas, como ondas, espirales y superficies orgánicas.
- Es la base para entender estructuras dinámicas y flexibles.
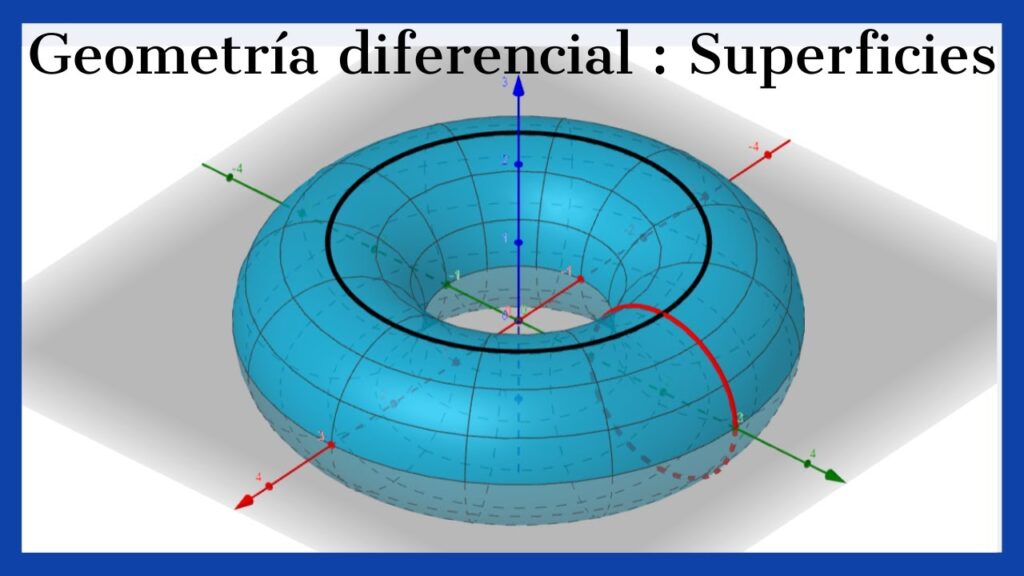
Este tipo de geometría resulta muy útil para modelar formas naturales, fluidas o abstractas, que escapan de la rigidez de la geometría clásica.
5. Geometría No Euclidiana
Surge en el siglo XIX, cuando se cuestionaron los postulados de Euclides, en especial el de las paralelas. Se divide en dos ramas principales:
- Geometría hiperbólica: plantea que por un punto externo a una recta pueden pasar infinitas paralelas. Genera un espacio curvo “abierto”.
- Geometría elíptica: establece que no existen rectas paralelas. Genera un espacio curvo “cerrado”.
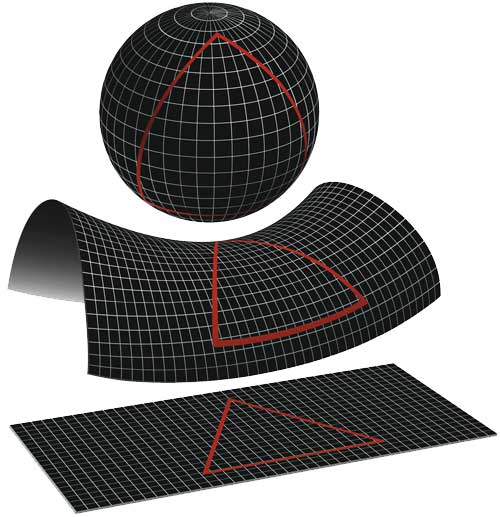
Estas geometrías abrieron la posibilidad de representar mundos no lineales, expandiendo la forma de concebir el espacio y anticipando incluso conceptos relacionados con la relatividad en física.
6. Geometría Fractal
Desarrollada en el siglo XX por Benoît Mandelbrot, estudia formas irregulares y autosimilares. Los fractales son figuras que se repiten en diferentes escalas, como sucede en la naturaleza (ramas de los árboles, nubes, montañas, venas en una hoja).

- Los fractales rompen con la idea de que la geometría solo describe formas perfectas.
- Permiten representar complejidad, caos organizado y patrones naturales.
- Se basan en iteraciones infinitas y en la autorreferencia de las formas.
7. Geometría Topológica
La topología, llamada también “geometría de la elasticidad”, se interesa más por las propiedades cualitativas que permanecen al deformar un objeto, sin importar medidas o ángulos.
- Un cuadrado puede convertirse en un círculo estirando sus lados sin romperlo.
- Una taza de café es equivalente a un donut (toro) porque ambos tienen un solo agujero.
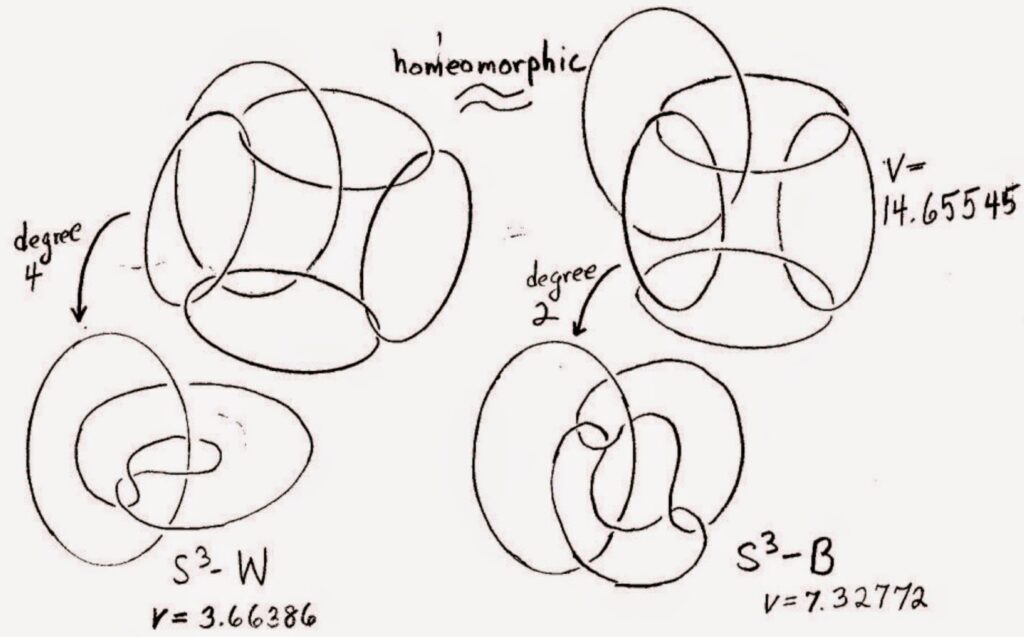
Este tipo de geometría es importante porque ofrece nuevas perspectivas para representar lo esencial de una forma, más allá de su apariencia exacta.
8. Geometría Computacional
Es una rama reciente que utiliza algoritmos y software para generar, manipular y analizar formas.
- Permite crear modelados 2D y 3D de alta complejidad.
- Se emplea en animación, videojuegos, realidad virtual, arquitectura y simulación.
- Facilita procesos creativos donde la precisión digital se combina con la libertad de experimentación.
Los distintos tipos de geometría no son compartimentos aislados, sino enfoques complementarios para comprender, representar y transformar el espacio y las formas. Desde la exactitud de la geometría euclidiana hasta la complejidad de los fractales o la flexibilidad de la topología, cada rama ofrece recursos que amplían el lenguaje visual, aportando tanto rigor como creatividad.