Propiedades geométricas
Los ángulos son una de las unidades fundamentales de la geometría. Se definen como la abertura formada por dos semirrectas que parten de un mismo punto llamado vértice. Más allá de su clasificación (agudos, rectos, obtusos, etc.), los ángulos poseen propiedades geométricas que permiten analizar relaciones espaciales, simetrías, transformaciones y estructuras tanto en geometría plana como en geometría aplicada (arquitectura, diseño, ingeniería).
Dentro de estas propiedades destacan la simetría y la conjugación, las cuales ayudan a comprender cómo se comportan los ángulos frente a ejes, giros y relaciones complementarias.
Simetría
Concepto de simetría
La simetría es una propiedad geométrica que describe la correspondencia exacta entre las partes de una figura respecto a un eje, un punto o un plano. En el caso de los ángulos, la simetría permite identificar cuándo dos ángulos son equivalentes en forma y medida, aunque se encuentren en posiciones opuestas o invertidas.
En términos simples, un ángulo es simétrico de otro cuando puede superponerse mediante una reflexión o giro.
Simetría axial en los ángulos
La simetría axial ocurre cuando un ángulo se refleja respecto a una recta llamada eje de simetría.
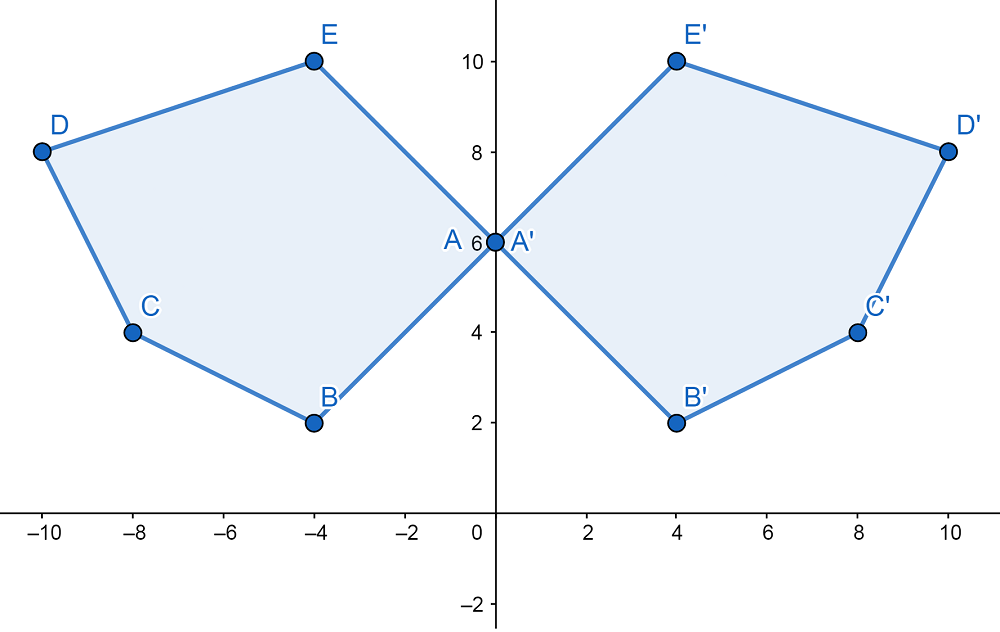
Características principales:
- El ángulo original y su simétrico tienen la misma medida.
- El vértice del ángulo permanece a la misma distancia del eje.
- Los lados del ángulo se reflejan formando el mismo ángulo con el eje, pero en sentido contrario.
Ejemplo:
Si un ángulo de 40° se refleja respecto a una recta vertical, el ángulo resultante también mide 40°, pero su orientación se invierte.
Aplicación:
La simetría axial es fundamental en:
- Diseño arquitectónico (fachadas simétricas)
- Diseño gráfico (composición equilibrada)
- Geometría descriptiva
Simetría central en los ángulos
La simetría central se produce cuando un ángulo se transforma mediante una rotación de 180° alrededor de un punto.
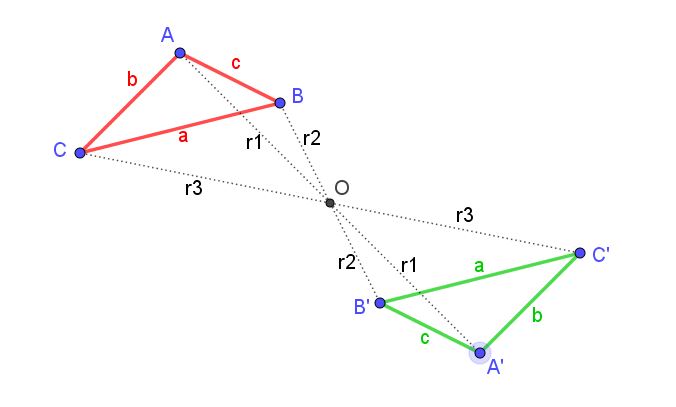
Propiedades:
- El ángulo conserva su medida.
- La orientación cambia completamente.
- El ángulo simétrico queda en posición opuesta al original.
Ejemplo:
Dos ángulos opuestos por el vértice son simétricos centrales.
Dato clave:
Los ángulos opuestos por el vértice siempre son iguales debido a esta simetría.
Importancia de la simetría en el estudio de ángulos
La simetría:
- Permite demostrar igualdad de ángulos sin necesidad de medirlos.
- Facilita el análisis de figuras complejas.
- Es base para comprender transformaciones geométricas más avanzadas.
Conjugación
Concepto de conjugación de ángulos
La conjugación se refiere a la relación que existe entre dos ángulos cuyas medidas están vinculadas por una suma constante, generalmente 180° o 360°. A estos ángulos se les llama ángulos conjugados.
En términos generales, un ángulo conjugado es aquel que completa a otro para formar un ángulo mayor.
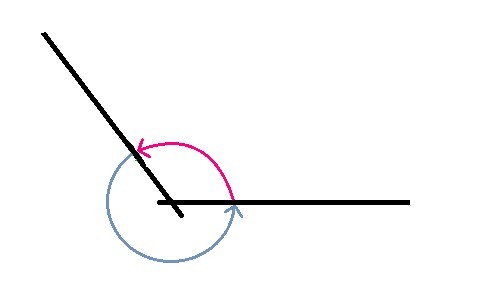
Ángulos conjugados suplementarios
Dos ángulos son conjugados suplementarios cuando la suma de sus medidas es igual a 180°.α+β=180°
Características:
- Forman una línea recta cuando son adyacentes.
- Si uno aumenta, el otro disminuye en la misma proporción.
- Son frecuentes en intersecciones de rectas.
Ejemplo:
Si un ángulo mide 65°, su conjugado suplementario mide:180°−65°=115°
Aplicación:
Se utilizan en:
- Geometría plana
- Análisis estructural
- Dibujo técnico
Ángulos conjugados explementarios
Dos ángulos son conjugados explementarios cuando la suma de sus medidas es 360°.α+β=360°
Características:
- Se relacionan con giros completos.
- Son importantes en geometría circular.
- Se usan en sistemas de coordenadas y trigonometría.
Ejemplo:
Si un ángulo mide 210°, su conjugado explementario mide:360°−210°=150°
Diferencia entre complementarios, suplementarios y conjugados
| Tipo de ángulo | Suma |
|---|---|
| Complementarios | 90° |
| Suplementarios | 180° |
| Conjugados (explementarios) | 360° |
Nota importante:
Todos los ángulos suplementarios son conjugados, pero no todos los conjugados son suplementarios.
Importancia de la conjugación en geometría
La conjugación:
- Permite resolver problemas sin medir ángulos directamente.
- Es clave en el estudio de rectas paralelas cortadas por una transversal.
- Se aplica en trigonometría, física y diseño estructural.
Conclusión
Las propiedades geométricas de los ángulos, específicamente la simetría y la conjugación, son herramientas esenciales para comprender las relaciones espaciales y estructurales dentro de la geometría. La simetría permite identificar equivalencias y transformaciones, mientras que la conjugación ayuda a entender cómo los ángulos se complementan dentro de sistemas más amplios.
Estas propiedades no solo tienen valor teórico, sino que son fundamentales en disciplinas como la arquitectura, el diseño, la ingeniería y la física, donde la precisión angular es clave para la estabilidad, la estética y la funcionalidad.




