1. Introducción al concepto de intersección
La intersección se refiere al punto, línea o conjunto de puntos donde una recta entra en contacto, atraviesa o corta un volumen. Cuando hablamos de volúmenes irregulares, nos referimos a cuerpos tridimensionales que no responden a formas geométricas simples (como cubos, cilindros o prismas), sino que presentan superficies curvas, inclinadas, asimétricas o combinaciones complejas de planos.
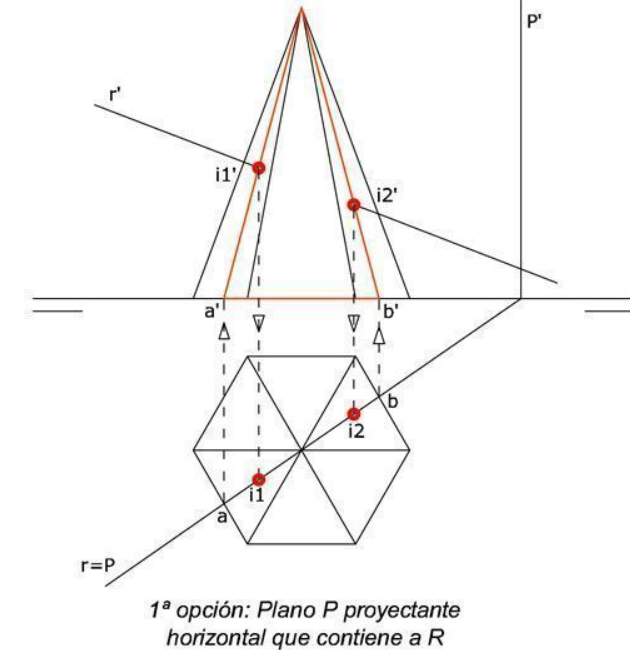
El estudio de estas intersecciones es fundamental en disciplinas como el dibujo técnico, la geometría descriptiva, la arquitectura, el diseño industrial y el modelado tridimensional, ya que permite comprender cómo se comportan los objetos en el espacio cuando son atravesados, cortados o relacionados con otros elementos lineales.
2. Naturaleza de los volúmenes irregulares
Los volúmenes irregulares presentan una serie de particularidades que influyen directamente en la forma de la intersección:

- Ausencia de simetría: la recta no produce resultados repetitivos o predecibles.
- Superficies mixtas: pueden coexistir planos, curvas convexas y cóncavas.
- Variación continua de la normal: el ángulo de incidencia de la recta cambia a lo largo del recorrido.
- Complejidad visual y geométrica: la intersección rara vez es un solo punto simple.
Estas características hacen que el análisis de la intersección requiera métodos auxiliares y una lectura espacial cuidadosa.
3. La recta como elemento intersector
La recta es un elemento geométrico de una sola dimensión que, al interactuar con un volumen, puede hacerlo de diversas maneras. Sus principales características en la intersección son:
- Dirección: horizontal, vertical u oblicua.
- Posición: frontal, lateral, superior o inferior respecto al volumen.
- Trayectoria: puede atravesar completamente el cuerpo o solo tocarlo.
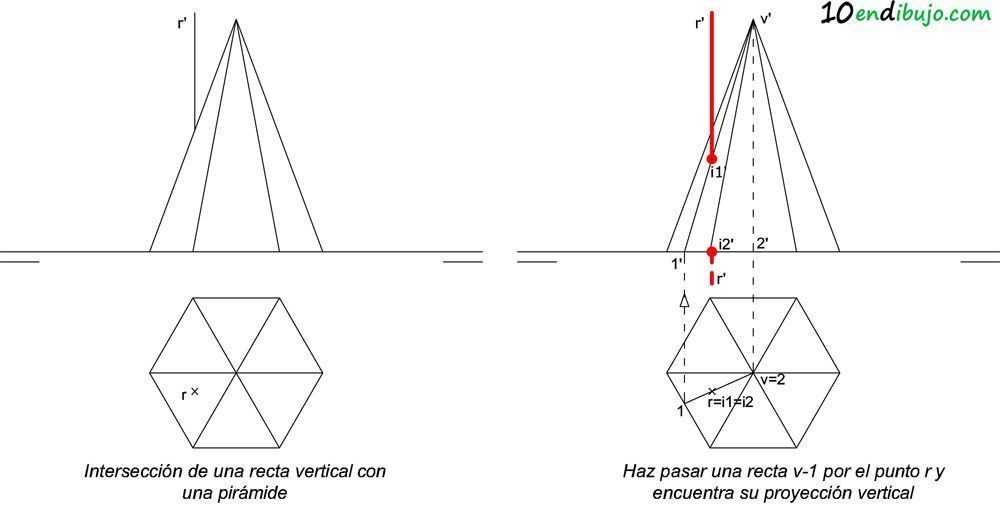
La recta funciona como un agente de análisis, permitiendo revelar la estructura interna o la forma real del volumen.
4. Tipos de intersección según la condición de contacto
a) Intersección puntual
Ocurre cuando la recta toca el volumen en un solo punto, generalmente en zonas tangenciales o vértices irregulares.
Características:
- No atraviesa el volumen.
- Es común en superficies curvas.
- Difícil de identificar sin proyecciones auxiliares.
b) Intersección secante
La recta entra y sale del volumen, generando dos o más puntos de intersección.
Características:
- Define un segmento interior invisible.
- Es la más común en análisis volumétrico.
- Permite estudiar espesores y profundidades.
c) Intersección tangencial
La recta coincide momentáneamente con la dirección de una superficie.
Características:
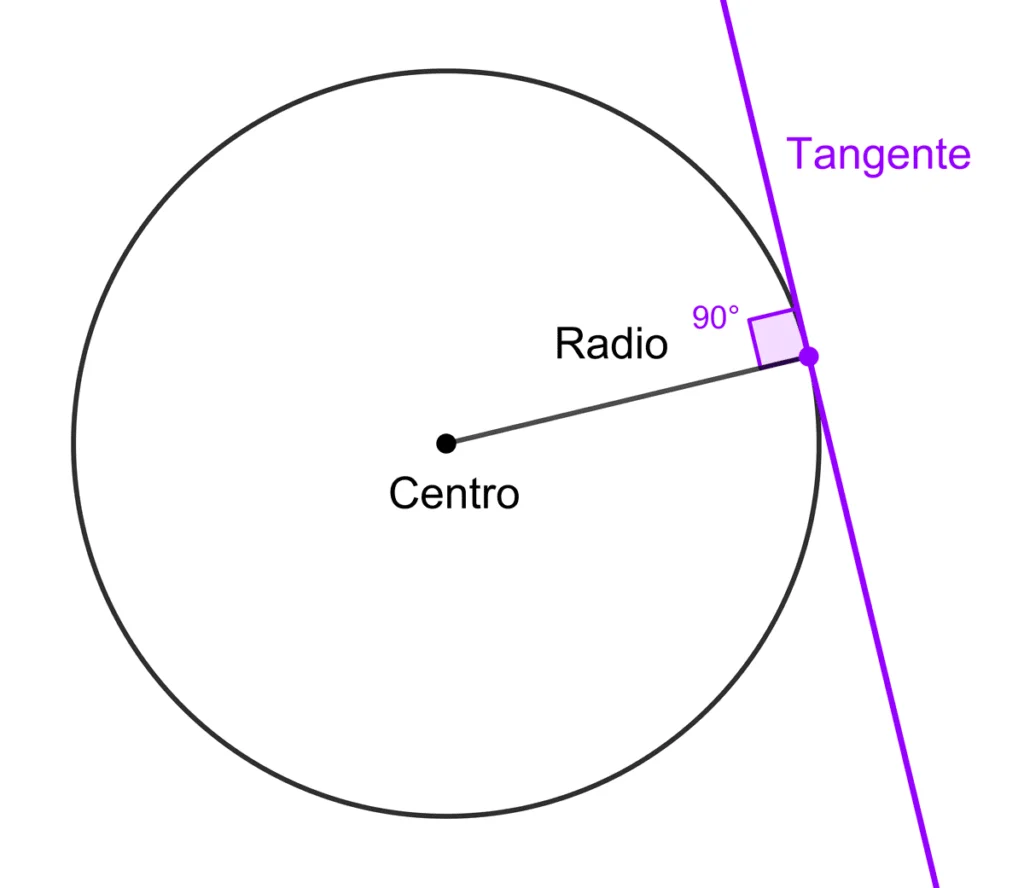
- El punto de contacto es crítico.
- Puede confundirse con una intersección secante si no se analiza correctamente.
- Muy frecuente en superficies curvas irregulares.
5. Influencia de la orientación de la recta
Recta paralela a un plano dominante
- Puede no intersectar el volumen.
- O generar intersecciones repetitivas y previsibles.
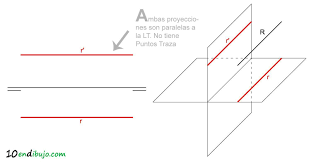
Recta oblicua
- Produce intersecciones complejas.
- Genera múltiples puntos de entrada y salida.
- Es la más utilizada para análisis completos del volumen.
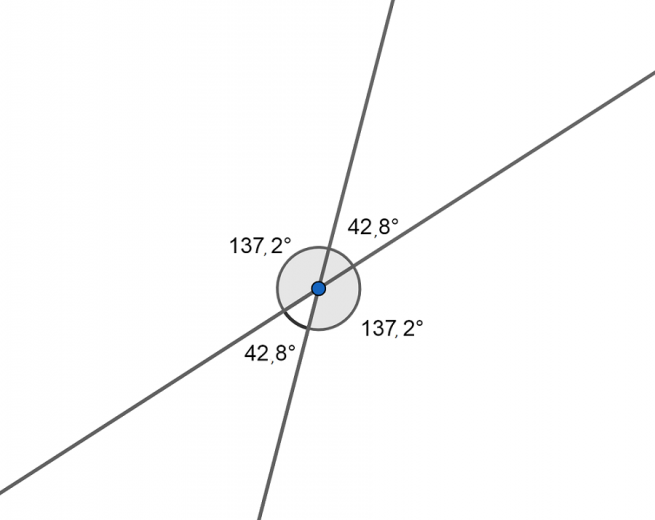
Recta perpendicular
- Facilita la lectura de profundidades.
- Produce intersecciones más claras, pero no siempre simples.
6. Representación gráfica de la intersección
En dibujo técnico, la intersección debe representarse mediante:
- Proyecciones ortogonales (alzado, planta y perfil).
- Líneas visibles e invisibles según la posición de la recta.
- Puntos de intersección reales y aparentes.
- Uso de líneas auxiliares para localizar puntos exactos.
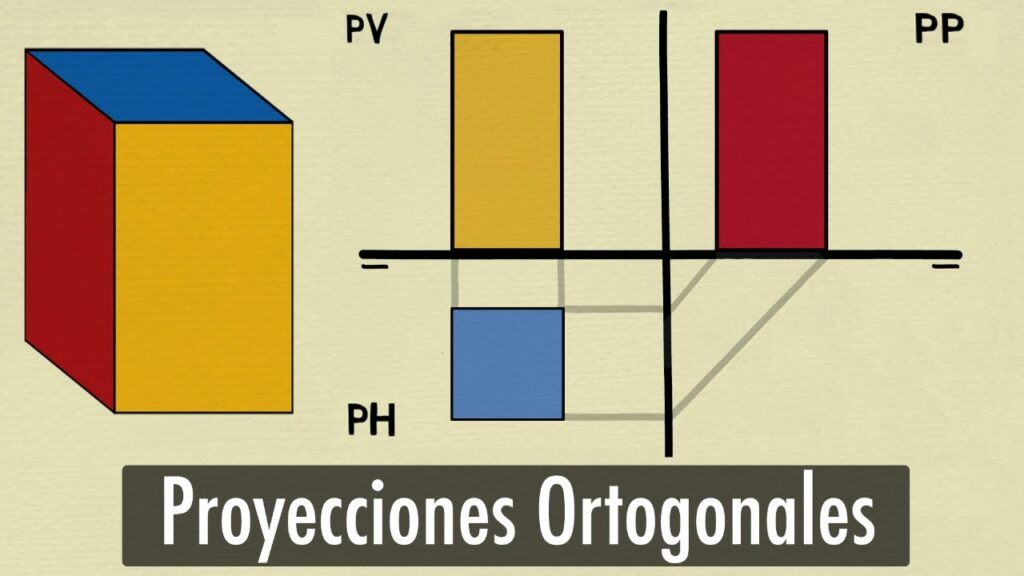
En volúmenes irregulares, rara vez la intersección se comprende en una sola vista; es necesario cruzar información visual.
7. Métodos de análisis y construcción
Método de planos auxiliares
Secciona el volumen con planos que contengan la recta, facilitando la localización de los puntos de intersección.
Método de generatrices
Especialmente útil en superficies curvas irregulares, permite identificar puntos comunes entre la recta y las líneas generadoras del volumen.
Método por aproximación gráfica
Se emplea en bocetaje, diseño conceptual y modelado, priorizando la comprensión visual sobre la exactitud matemática.
8. Importancia en diseño y arquitectura
La intersección de volúmenes irregulares con rectas es clave para:
- Diseño de estructuras complejas.
- Comprensión de cortes constructivos.
- Modelado de formas orgánicas.
- Desarrollo de objetos ergonómicos.
- Interpretación de trayectorias de luz, instalaciones o recorridos estructurales.
En arquitectura contemporánea, donde predominan las formas libres, este tipo de análisis es indispensable.
9. Errores comunes en el estudio de intersecciones
- Confundir intersección real con aparente.
- No considerar la profundidad del volumen.
- Omitir vistas auxiliares.
- Simplificar en exceso volúmenes complejos.
Estos errores afectan directamente la precisión del diseño y la lectura espacial.
10. Conclusión
El estudio de las intersecciones de volúmenes irregulares con rectas, en distintas condiciones, permite desarrollar una visión espacial avanzada, fundamental para el diseño, la arquitectura y la representación gráfica. No se trata solo de encontrar puntos de cruce, sino de entender el comportamiento tridimensional de la forma, su estructura interna y su relación con el espacio.
Dominar este tema implica combinar observación, análisis geométrico y representación gráfica, habilidades esenciales en la formación profesional del diseñador y arquitecto.