El uso de las escuadras en geometría

Las escuadras son instrumentos fundamentales dentro de la geometría, el dibujo técnico y el diseño. Se utilizan para la construcción precisa de ángulos, líneas y figuras geométricas, garantizando exactitud y limpieza en los trazos. Su aplicación no solo se limita al ámbito académico, sino que también es esencial en áreas como la arquitectura, la ingeniería, el diseño gráfico y la carpintería.

1. Tipos de escuadras

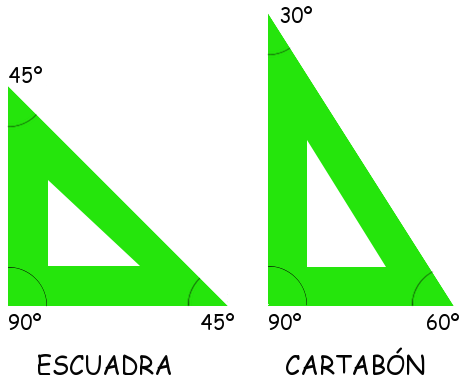
Existen principalmente dos tipos de escuadras empleadas en geometría:

1. Escuadra de 45° (isósceles):
   • Tiene forma de triángulo isósceles rectángulo.
   • Sus ángulos son de 45°, 45° y 90°.
   • Permite construir ángulos rectos y bisecar ángulos rectos con gran precisión.
2. Escuadra de 60°–30° (escalena):
   • Tiene forma de triángulo rectángulo escaleno.
   • Sus ángulos son de 30°, 60° y 90°.
   • Se utiliza para obtener divisiones en tercios y trazos más específicos.

Generalmente, ambas escuadras se usan en conjunto junto con la regla T o un borde de apoyo para lograr mayor exactitud en los trazados.

2. Funciones principales

Las escuadras cumplen diversas funciones dentro de la geometría:

1. Trazar líneas rectas y paralelas:
   Colocándolas sobre una regla T o el borde del papel, permiten dibujar rectas paralelas sin necesidad de medir.
2. Construcción de ángulos:
   • Escuadra de 45°: genera ángulos de 45° y 90°.
   • Escuadra de 30°–60°: genera ángulos de 30°, 60° y 90°.
   • Combinadas: permiten obtener otros ángulos como 15° o 75°.
3. Trazar perpendiculares:
   Apoyando una escuadra sobre otra se logran líneas perpendiculares exactas.
4. División de figuras geométricas:
   Se utilizan para dividir cuadrados, rectángulos y triángulos en partes iguales con gran precisión.
5. Construcción de polígonos regulares:
   Facilitan el trazado de hexágonos, triángulos equiláteros y otros polígonos sin necesidad de transportador.

3. Uso combinado de escuadras

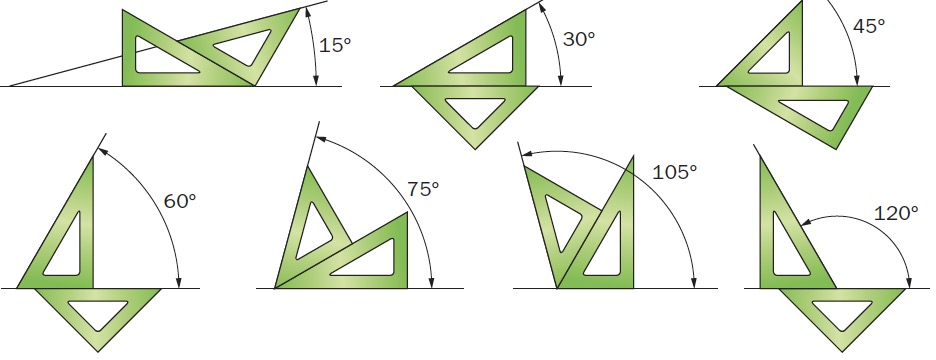
Cuando se superponen la escuadra de 45° y la de 30°–60°, se amplían las posibilidades de construcción:

• Se pueden obtener ángulos de 15°, 75° y 105°.
• Permiten reproducir ángulos sin necesidad de medir con transportador.
• Son útiles para crear tramas isométricas o perspectivas axonométricas en dibujo técnico.

4. Aplicaciones prácticas

• En geometría: construcción de figuras, análisis de simetrías y transformaciones.
• En dibujo técnico: elaboración de planos arquitectónicos e industriales.
• En diseño gráfico: estructuración de composiciones geométricas precisas.
• En carpintería: cortes y ensamblajes exactos en madera.
• En matemáticas escolares: aprendizaje de propiedades geométricas y resolución de ejercicios.

5. Recomendaciones para su uso

• Mantener las escuadras limpias y sin bordes dañados.
• Utilizarlas siempre apoyadas en un borde o regla T para garantizar precisión.
• Evitar presionar demasiado el lápiz, ya que puede alterar la línea.
• Complementarlas con compás y transportador para ampliar las construcciones geométricas.

El uso de las escuadras en geometría es esencial para garantizar exactitud en la construcción de ángulos, rectas y figuras. Su empleo desarrolla habilidades de precisión, orden y comprensión de la estructura geométrica, fundamentales tanto en la formación académica como en aplicaciones profesionales.